Boids
Optimisation Using Unsupervised Learning
Adam Price
May 14th 2020
In swarm intelligence, many individuals interact within a system. These individuals follow a set of simple rules, and through their interactions, more complex behaviour can emerge.
"The whole is greater than the sum of its parts"
- Probably Not Aristotle
A famous example of emergent behaviour is Craig Reynolds 'Boids' program. First created in 1986, the 'boids' simulate life-like flocking behaviour:

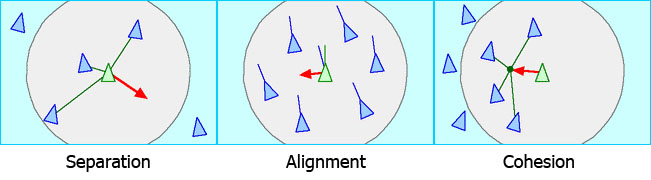
The movement of an entire flock looks complicated. However, if we consider the individuals, we can see that complex behaviour emerges from three simple rules:
- Separation: Boids move to avoid colliding with each other.
- Alignment: Boids steer to match the average direction of the boids around them.
- Cohesion: Boids move to towards the centre of the boids around them.
A single boid following these rules is computationally cheap. Nevertheless, basic implementations of the algorithm are highly inefficient. A boid needs to consider all other boids to calculate its velocity update. So, without additional programming, the boids algorithm has complexity $O(n^2)$ with respect to the number of boids. As we add more boids to the simulation, we exceptionally increase the workload.
Quick note: we are using a metric called 'slowdown' to measure performance. Essentially, slowdown is the ratio between the time it takes to create the simulation and real-time duration of that simulation.
A common way of increasing the performance of boids is through the use of spatial data structures. In the $O(n^2)$ algorithm, the boids consider all the other boids in the environment. However, their velocity update is only affected by the boids they are close to. Spatial data structures store the boids based on their positions. This lets only the boids that are stored together be compared, saving computations.
One of the most well-known spatial data structures is tiling. Tiling marks the locations of the boids by laying a set of tiles on the environment. Boids only consider other boids in their tiles and the tiles that surround it.

Tiling can improve the efficiency of Boids to near $O(n)$ with respect to the number of boids. However, an often overlooked issue of tiling is its efficiency in large state spaces. As the size of the 'world' that we hold our boids in increases, the number of tiles exponentially increases.
Calculating the velocity update of a boid has complexity $O(n)$ where n is the number of boids within range of the boid. Because of this, we would expect performance to improve in a more spacious (less boid dense) environment. Unfortunately, because tiling has exponential complexity in the state space size, it's performance doesn't improve much.
The solution that I propose to this problem is the use of an algorithm that has $O(n)$ complexity with respect to the size of the environment.
DBSCAN is an unsupervised learning clustering algorithm that produces clusters based on the density of the points. Applying DBSCAN to boids creates a set of sub-flocks that are too far apart to interact with each other. The boids in these sub-flocks, like in tiles, only need to consider other boids in the flock.

DBSCAN's performs significantly better than tiling in large state space. Tiling has to lay down many redundant tiles across the environment, many thousand in the most extreme cases. DBSCAN only needs to consider the boids locations as points so can cluster them quickly.
DBSCAN isn't necessarily a universal improvement. In high boid density situation, DBSCAN Boids has comparable performance to the $O(n^2)$ implementation. To address this, I have combined DBSCAN with the tiling algorithm previously discussed. The result is a version of the tiling algorithm that is far more efficient with respect to the size of the environment.

The red boxes show the areas of the environment where tiling updates are being performed. We can see that a small proportion of the environment requires updating between time steps. This gives a near-universal improvement over the original tiling approach as well as increased performance over plain DBSCAN in high boid density situations.
Although we have seen good improvement over the basic boids implementation, we have only dealt with improving the logic of the algorithm. Further performance increases could be found by optimising the code and using parallel programming.
